Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form
- a = x0 < x1 < x2 < ... < xn = b.
Such partitions are used in the theory of the Riemann integral, the Riemann–Stieltjes integral and the regulated integral. Another partition of the given interval, Q, is defined as a refinement of the partition, P, when it contains all the points of P and possibly some other points as well; the partition Q is said to be “finer” than P. Given two partitions, P and Q, one can always form their common refinement, denoted P ∨ Q, which consists of all the points of P and Q, re-numbered in order.
The norm (or mesh) of the partition
- x0 < x1 < x2 < ... < xn
is the length of the longest of these subintervals, that is
- max{ |xi − xi−1| : i = 1, ..., n }.
As finer partitions of a given interval are considered, their mesh approaches zero and the Riemann sum based on a given partition approaches the Riemann integral.
A tagged partition is a partition of a given interval together with a finite sequence of numbers t0, ..., tn−1 subject to the conditions that for each i,
- xi ≤ ti ≤ xi+1.
In other words, a tagged partition is a partition together with a distinguished point of every subinterval: its mesh is defined in the same way as for an ordinary partition. It is possible to define a partial order on the set of all tagged partitions by saying that one tagged partition is bigger than another if the bigger one is a refinement of the smaller one.
Suppose that 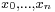 together with
together with 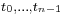 is a tagged partition of
is a tagged partition of ![[a, b]](/2012-wikipedia_en_all_nopic_01_2012/I/2c3d331bc98b44e71cb2aae9edadca7e.png) , and that
, and that 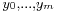 together with
together with 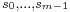 is another tagged partition of
is another tagged partition of ![[a,b]](/2012-wikipedia_en_all_nopic_01_2012/I/2c3d331bc98b44e71cb2aae9edadca7e.png) . We say that
. We say that 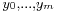 and
and 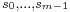 together is a refinement of a tagged partition
together is a refinement of a tagged partition 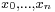 together with
together with 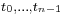 if for each integer
if for each integer  with
with 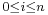 , there is an integer
, there is an integer 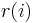 such that
such that 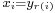 and such that
and such that 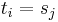 for some
for some  with
with 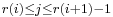 . Said more simply, a refinement of a tagged partition takes the starting partition and adds more tags, but does not take any away.
. Said more simply, a refinement of a tagged partition takes the starting partition and adds more tags, but does not take any away.